Resistors in
series! Ah! Just add their values and get the value of equivalent resistance. It's simple!But, wait a minute! What do we understand from equivalent resistance?
Equivalent
resistance is the resistance between the designated terminals of the network
that exhibits the same I-V characteristics as the original network. Apart from
this,
How do we
find equivalent resistance if the resistors are connected in parallel?
Is there a
method to calculate equivalent resistance of resistors in parallel?
The answer
to these questions lies in the article below –
Consider the
circuit given below:
Or
\[{{I}_{1}}=\frac{V}{{{R}_{1}}},{{I}_{2}}=\frac{V}{{{R}_{2}}},{{I}_{3}}=\frac{V}{{{R}_{3}}}\]
Applying KCL
at node a gives, I = I1+I2+I3
Putting the
value of each of the currents we get,
\[I=\frac{V}{{{R}_{1}}}+\frac{V}{{{R}_{2}}}+\frac{V}{{{R}_{3}}}=V\left(
\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}} \right)\]
Total
current $I=\frac{V}{Equivalent\text{ resistance}}=\frac{V}{{{R}_{eq}}}$
$\Rightarrow
\frac{V}{{{R}_{eq}}}=V\left(
\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}} \right)$ Or
$\frac{1}{{{R}_{eq}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}$
\[\Rightarrow
{{R}_{eq}}=\frac{{{R}_{1}}{{R}_{2}}{{R}_{3}}}{{{R}_{1}}{{R}_{2}}+{{R}_{2}}{{R}_{3}}+{{R}_{3}}{{R}_{2}}}\]
If there are
only two resistances in parallel, then
\[{{R}_{eq}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\]
The results
obtained above can be extended for N resistors in parallel, which can be stated
as follows:
\[\frac{1}{{{R}_{eq}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+............+\frac{1}{{{R}_{N}}}\]
And if, R1=R2=……..RN=R,
then ${{R}_{eq}}=\frac{R}{N}$
When
resistors are connected in parallel, it is more convenient to use conductance
rather than resistance. The equivalent conductance of N resistors in parallel
is Geq = G1+G2+G3+…..GN.
And
equivalent resistance Req can be determined from this as ${{R}_{eq}}=\frac{1}{{{G}_{eq}}}$
. Similarly, ${{G}_{1}}=\frac{1}{{{R}_{1}}},{{G}_{2}}=\frac{1}{{{R}_{2}}}$ ……
and so on.
With
conductance values given, it becomes easier to calculate equivalent conductance
and thereafter equivalent resistance.
IS THERE A WAY TO FIND CURRENTS THROUGH INDIVIDUAL RESISTANCES?
Yes, for
sure. And the principle used to find it is known as the current division
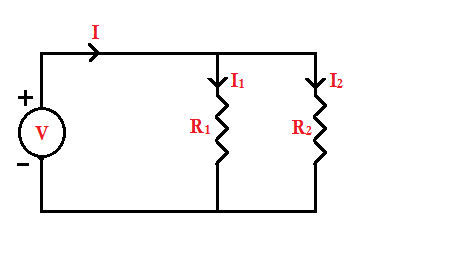
principle. To explain this, consider the following circuit:
\[{{R}_{eq}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\]
Now, from the figure, as the voltage across both the
resistors is same
\[{{I}_{1}}=\frac{V}{{{R}_{1}}},{{I}_{2}}=\frac{V}{{{R}_{2}}}\] …Equation 1
Voltage (V) of the circuit, V = IReq …..Equation 2
From Eq.1
and Eq.2, we get,
\[{{I}_{1}}{{R}_{1}}={{I}_{2}}{{R}_{2}}=I{{R}_{eq}}=V\]
\[\Rightarrow
{{I}_{1}}=\frac{I{{R}_{eq}}}{{{R}_{1}}}\]
Putting the value of Req calculated
before, we get
\[{{I}_{1}}=\left(
{}^{\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}}/{}_{{{R}_{1}}} \right)I\]
\[\Rightarrow
{{I}_{1}}=\left( \frac{{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}} \right)I\]
Similarly,${{I}_{2}}=\left(
\frac{{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}} \right)I$
This is the principle of current division and the circuit
used for this explanation is called a current divider circuit.
To best illustrate this principle, we will take up a
numerical example –
${{I}_{1}}=\frac{3}{9}\times 3=1A$ ;
${{I}_{2}}=\frac{6}{9}\times 3=2A$
Note that, the larger current (I2) flows
through the smaller resistance and the smaller current(I1) flows through the larger
resistance. This also proves the inverse proportionality of current and
resistance.
