THEVENIN'S THEOREM

Thevenin’s theorem was first proposed by a French telegraph engineer M.L.thevenin in 1883. Many a times we come across situations where we need to find the response (current, voltage, power) of a circuit against different values of load. Simplest example of this situation is in our homes; we connect different types of electrical devices (loads) to a single socket time and again. But then, what if we need to analyze the same circuit with different loads? It’s a tedious job you know!

WHAT THIS THEOREM DOES FOR US?

Thevenin’s theorem provides a mathematical technique for replacing a given network by a single voltage source with a series resistance, as viewed from the two output terminals.

STATEMENT:

Thevenin’s theorem states that a linear two terminal circuit can be replaced by an equivalent circuit consisting of a voltage source (V_th) in series with a resistor R_th, where

V_th – is the open circuit voltage as viewed from output terminals.

R_th – is the equivalent resistance at the terminals when the independent sources are turned off.

Thevenin’s theorem is a powerful tool in circuit analysis. It helps in replacing a large and complex circuit with a simple circuit consisting of voltage source and a series resistance.

HOW TO THEVENIZE A GIVEN CIRCUIT?

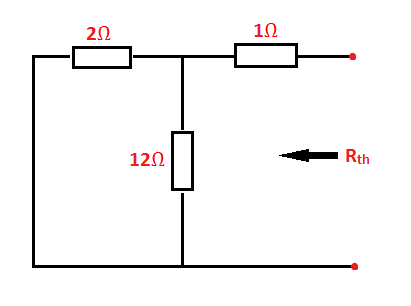
Consider the following circuit:

        1. Temporarily remove the load resistance R_L through which current is required.

        2. Compute the equivalent resistance as seen from the open terminals. Replace (turn off) independent voltage sources by short circuit and independent current sources by open circuit; and then calculate R_eq or R_th.
     

     NOTE: If the network has dependent sources, we turn off all independent sources, leaving the dependent sources intact, as they are controlled by circuit variables. In this case we can proceed in two ways to find R_th:

        1. Apply a voltage source V₀ at terminals a and b and determine the resulting current i₀. Then R_th=V₀/i₀.

   2. Insert a current source i₀ at terminals a – b and find terminal voltage V₀. Again R_th= V₀/i₀.In either approach we may assume any value of V₀ and i₀.

        3. Considering the circuit mentioned above with independent sources; after finding R_th,  find the open circuit voltage V_oc which appears across the two terminals a – b. This is V_th.

        4. Replace the entire network by a single thevenin source, whose voltage is V_th or V_oc and internal resistance R_th or R.

        5. Connect R_L back to its terminals from where it was previously removed.

        6. Finally, calculate the current flowing through R_L, using the equation –

I = V_th/(R_th+R_L)   or

I = V_oc/(R_i+R_L)

To find V_th –

Using mesh analysis,

$-16+2{{i}_{1}}+12({{i}_{1}}-{{i}_{2}})=0$ And ${{i}_{2}}=-1A$

Solving for i₁, we get

$-16+2{{i}_{1}}+12{{i}_{1}}+12=0$ 

$14{{i}_{1}}=4$ $\Rightarrow {{i}_{1}}=\frac{4}{14}=\frac{2}{7}$ .

${{V}_{th}}=12({{i}_{1}}-{{i}_{2}})=12(\frac{2}{7}+1)=12\times \frac{9}{7}=15.42V$